3 carrés inscrits dans le cercle de rayon R.

4 triangles équilatéraux inscrits dans le même cercle.

Les deux constructions réunies dans le même cercle
permettent de tracer un ennéagone
(polygone régulier inscrit de 9 côtés).

La démonstration mathématique est simple
et ne nécessite que quelques calculs trgonomètriques. Chacun sait que l'égalité exacte des aires est impossible, le nombre pi étant un nombre transcendant la construction exacte de racine de pi
est théoriquement impossible !

Encore faut-il prendre en compte le théorème de Gödel
qui a mis en évidence que :
« Il était impossible d’utiliser les axiomes des mathématiques pour prouver que ces axiomes
ne débouchaient jamais sur des contradictions. »
 
Tout carré inscrit dans le cercle circonscrit à l'ennéagone a une aire égale à celle du cercle primitif de rayon R 
avec une approximation de 14 millièmes.

C'est une résolution de

LA QUADRATURE DU CERCLE.

&&&

Vérification de la résolution de la quadrature du cercle :

 

 
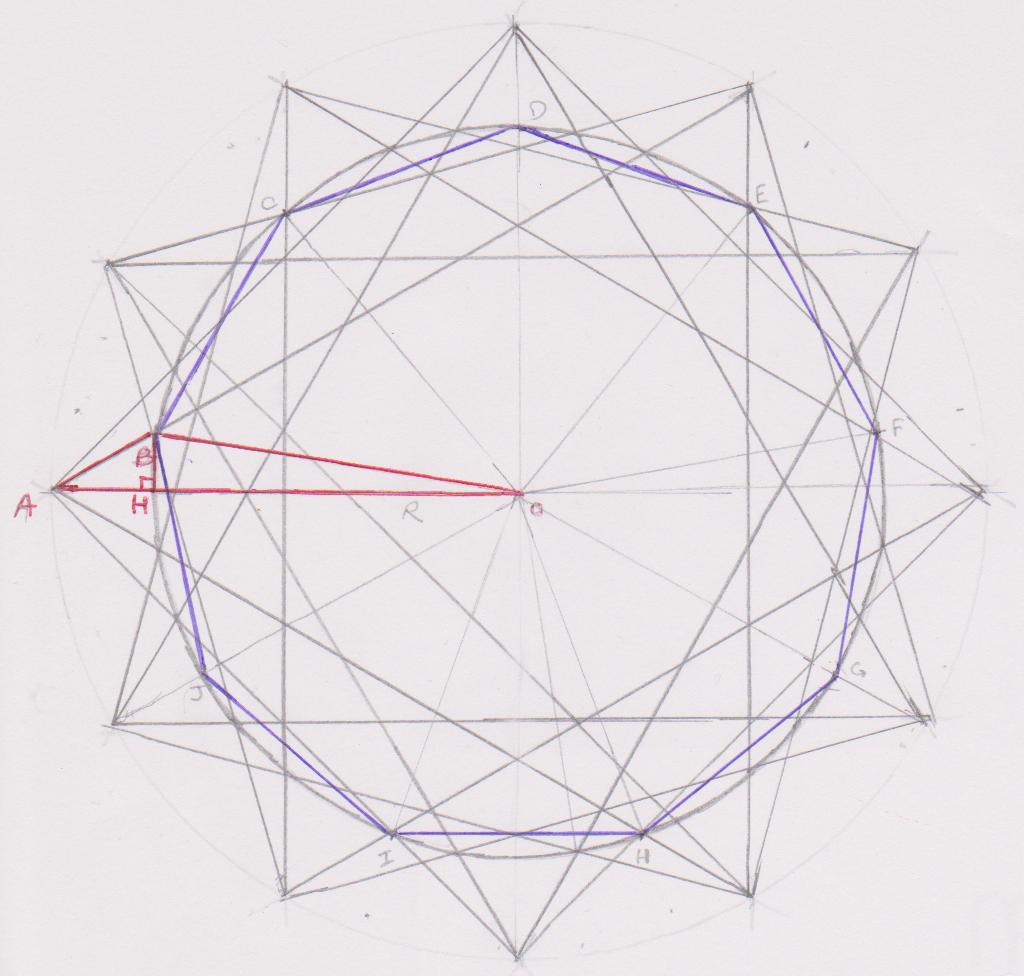
Soir R le rayon du plus grand cercle de centre O et C le côté du carré inscrit dans ce cercle.
L’aire de ce carré est donc : C² = 2R²
 
Aire du cercle circonscrit à l’ennéagone :

Soit R’ le rayon de ce cercle et OB sont rayon.

 

Dans le triangle OAB dont les angles OAB et BOA mesurent respectivement 30° et 20°, traçons la hauteur AH.
Dans le triangle OBH rectangle en H, nous avons :
R’cos20 = R – AH
La hauteur d'un triangle équilatéral de côté 1 est égale à rad.3/2
Dans le triangle ABH : AH = rad. 3/2 HB’
D’où : R’cos20 =R – AH = R – rad.3/2 x(R’x sin20)
Donc : R = (cos20 + rad3/2 x sin20) x R’
 
Si le carré et le cercle ont même aire, nous avons : 2 x R² = Pi x R’²
 
R = Rad Pi/ 2 x R’ = (cos20 + rad3/2 x sin20) x R’
Et Rad Pi/ 2 = (cos20 + rad3/2 x sin20)
 
En utilisant les tables trigonométriques on trouve :
Rad Pi/ 2 = 1,2533156... = 0,940 + 0,2996447 = 1,2396447 
Soit une différence de 0,0136709, moins de 13 millièmes !
 

&&&
 

  Voir « Travail sur La Quadrature du Cercle »

 &&&

Courriel de Hervé Laurent, auteur de :

"En quête du monde invisible", un livre d'Hervé Laurent, sourcier, géomètre, géobiologue et radiésthésiste

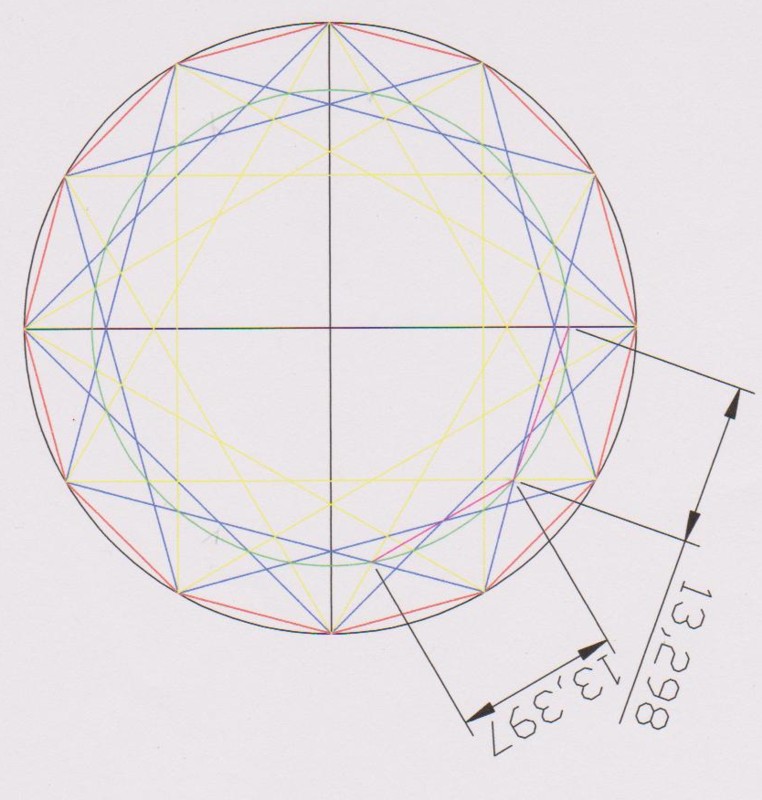
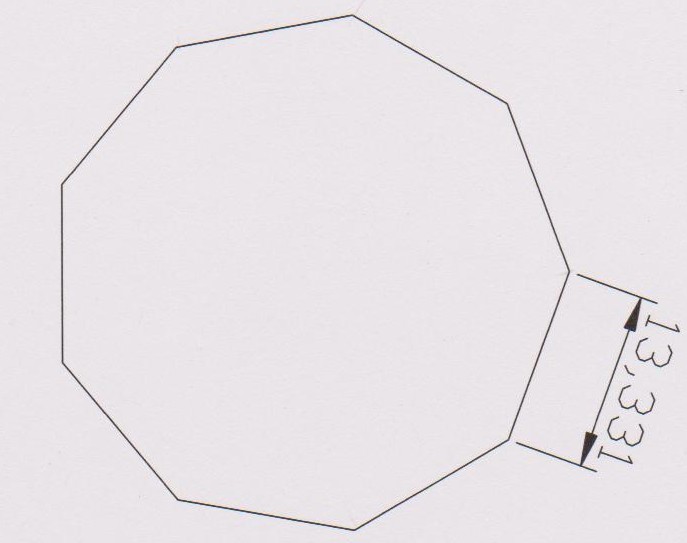
"J'ai tracé l'énnéagone avec autocad, mais en faisant "comme si" je n'utilisais que la règle et le compas (en construisnat au préalable l'angle de 30° par la bissectrice d'un triangle équilatéral)
Ce tracé est un tracé approché, bien suffisant pour un bâtisseur, mais inexact pour un géomètre
Voir sur le tracé joint en pdf les cotes des côtés

Belle journée"
Hervé

Avec l'autorisation d'hervé, je publie ses mesures :
 

Mes méthodes rudimentaires de dessin n’atteignent pas la précision du logiciel : c’est confondant ! Le résultat est suffisant en effet pour un bâtisseur ou un dessinateur. L'erreur oscille entre 33 et 66 millièmes !
J'ai utilisé la construction de Karuna sur la Voie du Mandala et elle m’a permis de charger ceux-ci d’une énergie très forte en ne me restreignant pas au déploiement des formes 2-4-8-16, 5-10-15, 3-6-12 et en permettant le 3-6-9-12.  
Comme dans une cathédrale, l’approximation n’empêche nullement la circulation d’une l’Energie opérative. Le géomètre se fait « Géo-Maître », la rigueur se déployant dans la souplesse. Le Point étant en toute rigueur sans dimension, toute construction est Vide, et pourtant pleine de tous les possibles…
Comme le précise l’Initiatrice de cette construction, il s’agit du Passage du cubique au sphérique, par l’approche de la résolution de la Quadrature du Cercle. Dans son Introduction, elle écrit :
« L’idée limitée à un seul point de vue qui fait dire que la Quadrature du Cercle est un faux problème ou un problème insoluble est une affirmation très limitative et quelque peu sommaire et ceci vient de ce qu’il n’est pas tenu compte de l’ajustement à la propre valeur de la figure. Il est donc nécessaire de savoir que, si c’est un problème à résoudre pour le non-connaissant, ce n’est en tout cas pas un faux problème… comme pour le mortel, réaliser son immortalité n’est pas pour lui illusoire, encore bien moins un but fallacieux. La comparaison entre la Quadrature et sa Circulation d’Energie est ici très illustrative, elle sert de base à cette étude comparative entre l’humain et le Cosmos, d’une part, et le mortel et son immortalité d’autre part. » (L’Instruction du Verseur d’Eau, p. 501) mais il faudrait citer tout le chapitre…
 
            Je ne connaissais pas cet Enseignement lors de la publication en auto-édition de « La Métaphysique des Chiffres. Tous les Chiffres ne disent qu’Unité. » ; l’un des chapitres est intitulé « Le Passage du 6 au 9 ». C’est lui qui est en jeu ici, passage de l’Humain au Divin, du corps de chair au Corps d’Immortalité (Corps de Gloire ou Corps Conscient). Les cathédrales et leurs cryptes de sous-terre sont des athanors alchimiques pour une telle transmutation.(en commençant déjà par faire de l’animal humain un Humain !) Les décodages le prouvent abondamment.

Astro-archéologue réputé, Robin Heath est chercheur honoraire de l'université du Pays de Galles, Lampeter. Auparavant, en tant que maitre de conférences et professeur, il a enseigné les mathématiques et les techniques de navigation.