2- La quête du saint Graal des mathématiques
Cette longue quête a été prise en relais par des générations de mathématiciens depuis plus de vingt siècles. Le pouls irrégulier de nombres premiers donna la fièvre à beaucoup ! Nous ne pouvons évoquer que les étapes les plus marquantes de cette saga incroyable.

Portrait de René Descartes par Frans Hals.
En 1637, René Descartes avait inventé la géométrie analytique. On veut souvent ignorer combien il s’est intéressé à la métaphysique, au point de publier en 1630 sa théorie de la création des vérités éternelles ; sa métaphysique se développe d’après ses réflexions sur la physique.
Pierre de Fermat a laissé son nom dans l’histoire des mathématiques à plus d’un titre. Le dernier théorème qu’il nota un jour à son réveil, vers 1621, en marge d’un livre, l’Arithmétique de Diophante, était accompagné de ces mots « J’ai découvert une preuve vraiment admirable de cette proposition ; mais cette marge est trop petite pour la contenir.(11) » Il s’agissait de démontrer, dit dans le langage actuel, qu’il n’existe aucun triplet de nombres entiers x, y et z satisfaisant la relation xn + yn = zn, où n représente un nombre entier supérieur à 2. Fermat mourut sans en dire plus sur cette preuve qui l’avait traversé dans une sorte de rêve éveillé et qu’il a sans doute été incapable de reconstituer. Sinon pourquoi ne l’eut-il pas fait ?
Son hypothèse joua un grand rôle dans la suite des travaux mathématiques, en particulier quant à la recherche des nombres premiers. Durant plus de trois siècles, elle tint en haleine les plus renommés des mathématiciens, parmi lesquels Euler, Lagrange et Riemann. Pourrait-on prouver l’énigme de Fermat ? Tous échouèrent à en apporter la démonstration ; elle fut considérée comme probable jusqu’à ce qu’elle soit résolue par Andrew Wiles de l'Université de Princeton (p. 265), avec l'aide de Richard Taylor. Après une première présentation en juin1993, puis la découverte d'une erreur et un an de travaux supplémentaires, la preuve fut finalement publiée en 1995.

Portrait de Pierre de Fermat.
Pythagore, en frappant une amphore pleine, puis vide à moitié, puis remplie successivement au tiers, au quart, au cinquième, etc. avait mis en évidence le lien entre musique et fractions. La série, dite harmonique, est représentée par la somme indéfinie : 1 + 1/2 + 1/3 + 1/4 +… + 1/n + …
Leonhard Euler, dans la première moitié du XVIIIe siècle, vit que cette suite ne pouvait être indéfinie que s’il y avait un nombre indéfini de nombres premiers (p. 129).
En donnant à x la valeur dans la fonction représentée par la lettre grecque zêta définie par :
Zêta(x) = 1/1x + 1/2x + 1/3x + … + 1/nx +… Euler obtint :
Zêta(2) = 1 + 1/4 + 1/9 + 1/16 +1/n2 + …
Cette somme était-elle indéfinie ou bien tendait-elle vers une valeur déterminée ? Il démontra qu’elle était égale à 1/6Pi carré, un développement anarchique et imprévisible introduit par pi (p.127).
Le produit d’Euler exprime cette fonction zêta de toute autre façon :
Zêta(x) = (1+ 1/2x + 1/4x + …) x (1+ 1/3x + 1/9x + …) x…(1+ 1/px + 1/(p2)x + …) x…
Leonhard Euler, dans la première moitié du XVIIIe siècle, vit que cette suite ne pouvait être indéfinie que s’il y avait un nombre indéfini de nombres premiers (p. 129).
En donnant à x la valeur dans la fonction représentée par la lettre grecque zêta définie par :
Zêta(x) = 1/1x + 1/2x + 1/3x + … + 1/nx +… Euler obtint :
Zêta(2) = 1 + 1/4 + 1/9 + 1/16 +1/n2 + …
Cette somme était-elle indéfinie ou bien tendait-elle vers une valeur déterminée ? Il démontra qu’elle était égale à 1/6Pi carré, un développement anarchique et imprévisible introduit par pi (p.127).
Le produit d’Euler exprime cette fonction zêta de toute autre façon :
Zêta(x) = (1+ 1/2x + 1/4x + …) x (1+ 1/3x + 1/9x + …) x…(1+ 1/px + 1/(p2)x + …) x…

Leonnhard Euler.
Il fallut un siècle « et l’intelligence de Dirichlet et de Riemann, pour que soit reconnue la force du produit d’Euler [qui reliait la fonction zêta aux nombres premiers]. Ce joyau des sciences grecques, contemplé sous une perspective du XIXe siècle, permettait de voir émerger un nouvel horizon mathématique que les Grecs n’auraient jamais pu imaginer » (p. 129).

Augustin Louis Cauchy.
Les nombres imaginaires (12) de Cauchy remplissaient alors de leur monde étrange l’esprit de Riemann ; ils pouvaient être associés à la fonction zêta (p. 130). « Il eut l’impression la conjecture de Gauss sur les nombres premiers était à portée de sa main » (p. 130). Karl Friedrich Gauss, à la fin du XVIIIe siècle, avait mis au point une formule qui, s’appuyant sur ce qu’il savait des nombres premiers jusqu’à 3 000 000, semblait toujours surestimer le nombre de nombres premiers (p. 93).

Karl Friedrich Gauss.
En 1859, Riemann, professeur à Göttingen, publie un article Sur les nombres premiers inférieurs à une grandeur donnée. Il redéfinit la fonction zêta en reprenant les travaux d’Euler et en les étendant aux nombres complexes ; il utilise cette fonction pour étudier la répartition des nombres premiers. La fonction zêta offrait à Riemann un miroir dans lequel le chaos apparent des nombres premiers s’ordonnait. Son hypothèse sur les zéros non triviaux de la fonction zêta passe alors inaperçue (p. 132).
Si pour Cauchy une fonction se définit par une équation, Riemann y ajouta un graphe. Mais comment représenter un graphe de la fonction zêta en quatre dimensions ? Cette quatrième dimension n’a rien à voir avec le temps. Les deux premières permettent de repérer les coordonnées des nombres imaginaires que l’on entre dans la fonction zêta (p. 136). La troisième et la quatrième dimensions enregistrent les deux coordonnées décrivant le nombre imaginaire produit par la fonction (id.). Le graphe ne peut représenter que l’ombre tridimensionnelle d’un paysage à quatre dimensions.
Si pour Cauchy une fonction se définit par une équation, Riemann y ajouta un graphe. Mais comment représenter un graphe de la fonction zêta en quatre dimensions ? Cette quatrième dimension n’a rien à voir avec le temps. Les deux premières permettent de repérer les coordonnées des nombres imaginaires que l’on entre dans la fonction zêta (p. 136). La troisième et la quatrième dimensions enregistrent les deux coordonnées décrivant le nombre imaginaire produit par la fonction (id.). Le graphe ne peut représenter que l’ombre tridimensionnelle d’un paysage à quatre dimensions.
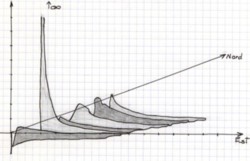
Aperçu sur le paysage zéta de Riemmann
et qu'il fallait poursuivre vers l'est.
Les « paysages » que « voient » les mathématiciens lorsqu’ils se représentent la fonction zêta en quatre dimensions sont fabuleux (p.138-140). Une topographie déconcertante révèle un réel totalement inattendu puisque, comme dans cet hologramme, n’importe quelle petite région peut permettre de reconstituer l’ensemble (p.141).
Ce paysage recouvrait toute la carte des nombres imaginaires (p. 141). Il était « inflexible ». Toutes « les collines et les vallées d’une région contenaient des informations sur la topographie de l’ensemble du décor » (id.). « Tout cartographe mathématicien capable de repérer sur la carte bidimensionnelle les points où le relief atteignait le niveau de la mer serait en mesure de reconstituer l’ensemble du paysage » (id.). Et « dans ces paysages imaginaires, l’emplacement de tous les nombres imaginaires là où la fonction donne zéro vous dit tout ». Ce sont les « zéros » de la fonction zêta (p. 142). Quel lien peut-il exister entre les nombres premiers et les zéros obtenus ?
Le génie de Riemann fut de montrer que les nombres premiers et les zéros étaient les deux pans d’une même équation (id.).
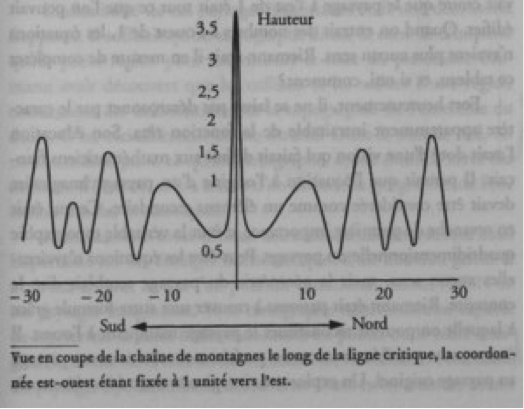
Même affinée par rapport à la fonction de Gauss, la méthode de Riemann n’est pas absolument exacte, elle laisse « une marge d’erreur d’un millième pour cent » (p. 143) pour prévoir le nombre de nombres premiers compris entre 1 et N. Voilà que sur les graphes, la courbe en escalier devient une courbe lisse qui se trouve secouée par les ondes lorsque sont « ajoutées les erreurs prédites par les trente premières ondes nées des trente premiers zéros » rencontrés (p. 146). « Riemann avait identifié ce qui contrôlait les infimes détails des nombres premiers » (p. 148).
L’image des nombres premiers chaotiques dans le miroir qui séparait le monde des nombres de son paysage zêta était un ordre strict de zéros, alignés sur une droite (p. 157). Cette droite critique passait par ½. L’hypothèse est que tous les zéros se trouvent sur cette droite, mais ils sont en nombre indéfini et personne jusqu’à ce jour n’a pu en apporter la preuve ! Si son hypothèse était juste, « cela impliquait que l’estimation de Gauss serait toujours d’une incroyable précision » (p. 159).
Euler avait découvert qu’en rentrant un nombre imaginaire dans une fonction exponentielle, on obtenait une onde sinusoïdale (p. 144). Riemann « voyait comment chacun de ces points pouvait être transformé en une onde particulière à l’aide de la fonction zêta » (id.). Ainsi les nombres premiers se métamorphosaient pour créer le paysage zêta, « et les points situés au niveau de la mer dans ce paysage sont les clés qui permettent d’en déchiffrer le secret » (p.145). « Riemann comprit que, quand on aurait ajouté le nombre infini d’ondes, une pour chaque point au niveau de la mer qu’il croiserait en progressant vers le nord du paysage zêta, la courbe finale ressemblerait exactement à l’escalier de nombres premiers » (p. 146). Il « avait dévoilé les archives contenant les billets gagnants de la loterie des nombres premiers » (p. 148) ! Il y avait une structure harmonique cachée.
Pour David Hilbert, l’hypothèse de Riemann était le problème le plus important dans l’absolu (p. 181).
Riemann avait procédé à une quantité incroyable de calculs arithmétiques purs. Carl Ludwig Siegel, au début du XXe siècle, réussit l’exploit de comprendre ce qui avait été fait : Riemann avait ainsi calculé des zéros. Il a « su extraire la formule du capharnaüm des notes de Riemann » (p. 238) et celle-ci porte justement le nom de « formule de Riemann-Siegel ».
En 1912, John Edensor Littlewood démontra qu’au lieu de surestimer le nombre de nombres premiers, l’hypothèse de Gauss, jusque là non prouvée, les sous-estimait (p 202). Il prouva également « que l’ajustement de Riemann pouvait sembler plus exact pour les premiers millions de nombres premiers, mais dans les marches plus éloignées de l’univers des nombres, il arrivait parfois que l’estimation de Gauss soit plus juste » (p. 202). La démonstration « révélait que les nombres premiers sont passés maîtres dans l’art du camouflage. Ils dissimulaient leur véritable nature dans les replis insondables de l’univers des nombres, si profondément que l’humanité ne disposera peut-être jamais des capacités de calcul nécessaires pour observer leur essence réelle » (pp. 204-205).
Le génie de Riemann fut de montrer que les nombres premiers et les zéros étaient les deux pans d’une même équation (id.).
Même affinée par rapport à la fonction de Gauss, la méthode de Riemann n’est pas absolument exacte, elle laisse « une marge d’erreur d’un millième pour cent » (p. 143) pour prévoir le nombre de nombres premiers compris entre 1 et N. Voilà que sur les graphes, la courbe en escalier devient une courbe lisse qui se trouve secouée par les ondes lorsque sont « ajoutées les erreurs prédites par les trente premières ondes nées des trente premiers zéros » rencontrés (p. 146). « Riemann avait identifié ce qui contrôlait les infimes détails des nombres premiers » (p. 148).
L’image des nombres premiers chaotiques dans le miroir qui séparait le monde des nombres de son paysage zêta était un ordre strict de zéros, alignés sur une droite (p. 157). Cette droite critique passait par ½. L’hypothèse est que tous les zéros se trouvent sur cette droite, mais ils sont en nombre indéfini et personne jusqu’à ce jour n’a pu en apporter la preuve ! Si son hypothèse était juste, « cela impliquait que l’estimation de Gauss serait toujours d’une incroyable précision » (p. 159).
Euler avait découvert qu’en rentrant un nombre imaginaire dans une fonction exponentielle, on obtenait une onde sinusoïdale (p. 144). Riemann « voyait comment chacun de ces points pouvait être transformé en une onde particulière à l’aide de la fonction zêta » (id.). Ainsi les nombres premiers se métamorphosaient pour créer le paysage zêta, « et les points situés au niveau de la mer dans ce paysage sont les clés qui permettent d’en déchiffrer le secret » (p.145). « Riemann comprit que, quand on aurait ajouté le nombre infini d’ondes, une pour chaque point au niveau de la mer qu’il croiserait en progressant vers le nord du paysage zêta, la courbe finale ressemblerait exactement à l’escalier de nombres premiers » (p. 146). Il « avait dévoilé les archives contenant les billets gagnants de la loterie des nombres premiers » (p. 148) ! Il y avait une structure harmonique cachée.
Pour David Hilbert, l’hypothèse de Riemann était le problème le plus important dans l’absolu (p. 181).
Riemann avait procédé à une quantité incroyable de calculs arithmétiques purs. Carl Ludwig Siegel, au début du XXe siècle, réussit l’exploit de comprendre ce qui avait été fait : Riemann avait ainsi calculé des zéros. Il a « su extraire la formule du capharnaüm des notes de Riemann » (p. 238) et celle-ci porte justement le nom de « formule de Riemann-Siegel ».
En 1912, John Edensor Littlewood démontra qu’au lieu de surestimer le nombre de nombres premiers, l’hypothèse de Gauss, jusque là non prouvée, les sous-estimait (p 202). Il prouva également « que l’ajustement de Riemann pouvait sembler plus exact pour les premiers millions de nombres premiers, mais dans les marches plus éloignées de l’univers des nombres, il arrivait parfois que l’estimation de Gauss soit plus juste » (p. 202). La démonstration « révélait que les nombres premiers sont passés maîtres dans l’art du camouflage. Ils dissimulaient leur véritable nature dans les replis insondables de l’univers des nombres, si profondément que l’humanité ne disposera peut-être jamais des capacités de calcul nécessaires pour observer leur essence réelle » (pp. 204-205).

John Edensor Littlewood
Beaucoup de mathématiciens se sont passionnés pour la recherche des nombres premiers. Certains, comme Landau, Hardy et Littlewood manifestent de sérieux doutes et vont jusqu’à croire que l’hypothèse de Riemann est fausse (p. 233).
Et le Norvégien Arle Selberg de dire « Je suis convaincu qu’on finira par trouver la solution. Je ne crois pas que le résultat soit indémontrable. Mais peut-être la preuve est-elle si complexe que le cerveau humain n’arrivera pas à l’appréhender » (p. 269).
Selberg se plongeant dans la recherche tomba sur un article de l’Indien Ramanujan et fut frappé par ses « formules étrangement belles » (p. 244). Ramanujan parvint à démontrer « qu’entre 5 et 10% des zéros obéissaient à l’hypothèse de Riemann » (p. 247). Selberg, séduit par la simplicité et la beauté des formules, pensait qu’elles pouvaient « déboucher sur la distribution naturelle des nombres premiers. On se dit qu’il y a au moins une chose qui pourrait y être correcte dans cet univers » (p. 248). Alors que, pour Hardy, les nombres premiers portaient en eux « une malice diabolique » (p. 250) !
Le Hongrois Paul Erdös, lui, traitait Dieu de « fasciste suprême » (cité p. 251), le voyant comme le gardien « du Grand Livre qui recelait les détails de toutes les démonstrations élégantes des problèmes mathématiques, résolus ou non » (p. 251) ! Il entretint l’idée d’une rencontre entre la théorie des nombres premiers et celle des probabilités (p. 256).
Et le Norvégien Arle Selberg de dire « Je suis convaincu qu’on finira par trouver la solution. Je ne crois pas que le résultat soit indémontrable. Mais peut-être la preuve est-elle si complexe que le cerveau humain n’arrivera pas à l’appréhender » (p. 269).
Selberg se plongeant dans la recherche tomba sur un article de l’Indien Ramanujan et fut frappé par ses « formules étrangement belles » (p. 244). Ramanujan parvint à démontrer « qu’entre 5 et 10% des zéros obéissaient à l’hypothèse de Riemann » (p. 247). Selberg, séduit par la simplicité et la beauté des formules, pensait qu’elles pouvaient « déboucher sur la distribution naturelle des nombres premiers. On se dit qu’il y a au moins une chose qui pourrait y être correcte dans cet univers » (p. 248). Alors que, pour Hardy, les nombres premiers portaient en eux « une malice diabolique » (p. 250) !
Le Hongrois Paul Erdös, lui, traitait Dieu de « fasciste suprême » (cité p. 251), le voyant comme le gardien « du Grand Livre qui recelait les détails de toutes les démonstrations élégantes des problèmes mathématiques, résolus ou non » (p. 251) ! Il entretint l’idée d’une rencontre entre la théorie des nombres premiers et celle des probabilités (p. 256).

Paul Erdös
A cette époque, des physiciens avancèrent « l’idée que le hasard faisait partie intégrante du monde subatomique » (p. 256). « Tandis qu’Einstein s’efforçait de nier que Dieu jouait aux dés avec la Nature (…) Erdös, lui, démontrait que les lancers de dés étaient au cœur de la théorie des nombres » (p. 257). Au vrai, il s’intéressait aussi au lancer des pièces de monnaie. « Une pièce normale présente un comportement authentiquement aléatoire (p. 259). « Pour démontrer que les nombres premiers sont vraiment aléatoires, il faut d’abord prouver que de l’autre côté du miroir de Riemann, les zéros sont agencés le long de la fameuse droite » (id.). Il fallait revenir « à la partie concrète du miroir de Riemann. » (p. 260) On ne pouvait progresser sans le recours aux idées de Riemann (p. 261).
Tous ceux qui se sont attaqués à l’hypothèse de Riemann se sont cassés les dents, quelles que soient les avancées produites ! « Weil [André, frère de Simone Weil] avait utilisé un étrange tambour mathématique pour naviguer dans son paysage longtemps avant même que les connexions avec la physique quantique nous prouvent que c’était la bonne façon de procéder dans la recherche d’une solution » (p. 456). Ce nouveau phare, certes, éclaire le paysage, mais on en est encore réduit pour aller de l’avant à accepter l’hypothèse de Riemann et, si elle se révélait fausse, toutes les déductions s’écrouleraient.
Tous ceux qui se sont attaqués à l’hypothèse de Riemann se sont cassés les dents, quelles que soient les avancées produites ! « Weil [André, frère de Simone Weil] avait utilisé un étrange tambour mathématique pour naviguer dans son paysage longtemps avant même que les connexions avec la physique quantique nous prouvent que c’était la bonne façon de procéder dans la recherche d’une solution » (p. 456). Ce nouveau phare, certes, éclaire le paysage, mais on en est encore réduit pour aller de l’avant à accepter l’hypothèse de Riemann et, si elle se révélait fausse, toutes les déductions s’écrouleraient.

André Weil
Notes :
11 - Cité dans L’Histoire universelle des chiffresde Georges Ifrah, Ed. Robert Laffont, 1994, tome II, p.752.
12 - Cauchy, né en 1789, après la prise de la Bastille, poussa les mathématiques pures si loin qu’il passait pour fou. Il imagina un nombre qui serait la racine carrée de –1 ! « Les nombres imaginaires [qui en découlent] détiennent la clé du monde des particules subatomiques découvert au XXe siècle. » Jamais les aéroplanes n’auraient volé si les ingénieurs n’avaient exploré cet outil. (p. 106)
12 - Cauchy, né en 1789, après la prise de la Bastille, poussa les mathématiques pures si loin qu’il passait pour fou. Il imagina un nombre qui serait la racine carrée de –1 ! « Les nombres imaginaires [qui en découlent] détiennent la clé du monde des particules subatomiques découvert au XXe siècle. » Jamais les aéroplanes n’auraient volé si les ingénieurs n’avaient exploré cet outil. (p. 106)
